Longitud de Arco

Bahena Sosa Cesar Armando

Clase del 26 de Octubre 2024

Profe. Alejandro Gómez

Tema: Longitud de arco

Conocimiento Consultado:

Uso del Cálculo para encontrar la longitud de una curva.

Imagina que queremos encontrar la longitud de una curva entre dos puntos. Y la curva es suave (la derivada es continua).

Primero dividimos la curva en pequeñas longitudes y usamos la fórmula de Distancia entre dos puntos en cada longitud para obtener una respuesta aproximada:

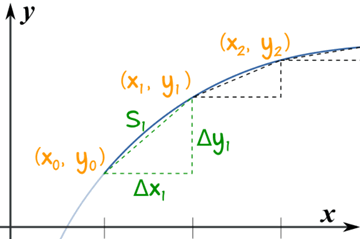
La distancia de x0 a x1 es:

S1 = √ (x1 − x0)2 + (y1 − y0)2

Y sea Δ (delta) la diferencia entre valores, de modo que tenemos:

S1 = √ (Δx1)2 + (Δy1)2

Ahora solo necesitamos muchos más segmentos:

S2 = √(Δx2)2 + (Δy2)2
S3 = √(Δx3)2 + (Δy3)2
...
...
Sn = √(Δxn)2 + (Δyn)2

 

Podemos escribir todas esas líneas en una sola línea usando una Suma:

S ≈ 

n

i=1

 √(Δxi)2 + (Δyi)2

¡Pero todavía estamos condenados a una gran cantidad de cálculos!

Tal vez podamos hacer una hoja de cálculo grande o escribir un programa para hacer los cálculos ... pero intentemos algo más.

Tenemos un plan astuto:

• hagamos que todos los Δxi sean iguales para que podamos extraerlos del interior de la raíz cuadrada
• y luego convertir la suma en una integral.

Hagámoslo:

Primero, dividamos y multipliquemos Δyi por Δxi:

S ≈ 

n

i=1

 √(Δxi)2 + (Δxi)2(Δyi/Δxi)2

Ahora factorizamos (Δxi)2:

S ≈ 

n

i=1

 √(Δxi)2(1 + (Δyi/Δxi)2)

Sacmos (Δxi)2 de la raíz cuadrada:

S ≈ 

n

i=1

 √1 + (Δyi/Δxi)2  Δxi

Ahora, a medida que n tiende a infinito (a medida que nos dirigimos hacia un número infinito de cortes, y cada corte se vuelve más pequeño) obtenemos:

S = 

lim

n→∞

 

n

i=1

 √1 + (Δyi/Δxi)2  Δxi

Ahora tenemos una integral y escribimos dx para indicar que los cortes Δx se acercan a un ancho cero (lo mismo para dy):

S = 

b

a

 √1+(dy/dx)2 dx

Y dy/dx es la derivada de la función f(x), que también se puede escribir f’(x):

S = 

b

a

 √1+(f’(x))2 dx
La Fórmula de Longitud de Arco

Y ahora, de repente, estamos en una posición mucho mejor, no necesitamos sumar muchos cortes, podemos calcular una respuesta exacta (si podemos resolver el diferencial y la integral).

Nota: la integral también funciona con respecto a y, útil si conocemos x = g(y):

S = 

d

c

 √1+(g’(y))2 dy

Así que los pasos a seguir son:

• Encontrar la derivada de f’(x)
• Resolver la integral de √1 + (f’(x))2 dx

Video relacionado al tema:

https://www.youtube.com/watch?v=iCNOdf6xF5I

Imagen:

Referencias: 

https://www.disfrutalasmatematicas.com/calculo/longitud-arco.html 

https://www.youtube.com/watch?v=iCNOdf6xF5I